Bachmann–Howard ordinal
In mathematics, the Bachmann–Howard ordinal (or Howard ordinal) is a large countable ordinal. It is the proof theoretic ordinal of several mathematical theories, such as Kripke–Platek set theory (with the axiom of infinity) and the system CZF of constructive set theory. It is named after William Alvin Howard and Heinz Bachmann.
Definition
The Bachmann–Howard ordinal is defined using an ordinal collapsing function (with more details given in the relevant article):
- εα enumerates the epsilon numbers, the ordinals ε such that ωε = ε.
- Ω = ω1 is the first uncountable ordinal.
- εΩ+1 is the first epsilon number after Ω = εΩ.
- ψ(0) is defined to be the smallest ordinal that cannot be constructed by starting with 0, 1, ω and Ω, and repeatedly applying ordinal addition, multiplication and exponentiation.
- ψ(α) is defined in the same way, except that it also allows applications of ψ to previously constructed ordinals less than α.
- The Bachmann–Howard ordinal is ψ(εΩ+1).
The Bachmann–Howard ordinal can also be defined as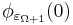 
for an extension of the Veblen functions φα to uncountable α; this extension is not completely straightforward.
References
- Bachmann, Heinz (1950), "Die Normalfunktionen und das Problem der ausgezeichneten Folgen von Ordnungszahlen", Vierteljschr. Naturforsch. Ges. Zürich 95: 115–147, MR0036806
- Howard, W. A. (1972), "A system of abstract constructive ordinals.", J. Symbolic Logic (Association for Symbolic Logic) 37 (2): 355–374, doi:10.2307/2272979, JSTOR 2272979, MR0329869
- Pohlers, Wolfram (1989), Proof theory, Lecture Notes in Mathematics, 1407, Berlin: Springer-Verlag, ISBN 3-540-51842-8, MR1026933
- Rathjen, Michael (August 2005). "Proof Theory: Part III, Kripke-Platek Set Theory". http://www.mathematik.uni-muenchen.de/~aehlig/EST/rathjen4.pdf. Retrieved 2008-04-17. (slides of a talk given at Fischbachau)
|
|||||